Constructive Solid Geometry

When the hardware accelerator provided by Apple Computer, Inc., is available, the interactive renderer can support constructive solid geometry (CSG), a method of modeling solid objects constructed from the union, intersection, or difference of other solid objects. For instance, you can define two cubes and then render the solid object that is the intersection of those two cubes. Similarly, you can define three cubes and render the solid object that is the union of two of them minus the third. For example, Figure 3 shows three cubes ( A , B , and C ) together with the result of using CSG to create the solid object defined by the function ( A B ) ¬ C .

In this chapter, CSG operations are described using standard set operators: the operation A B is the set of all points that are in both A and B (that is, the intersection of A and B ); A B is the set of all points that are in either A or B (that is, the union of A and B ); ¬ A is the set of all points that are not in A (that is, the complement of A ).

Figure 3 A constructed CSG object

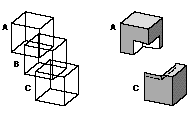
The interactive renderer supports CSG operations on up to five objects in a model. You select the objects to operate on by assigning a CSG object ID to an object, an attribute of type kQ3AttributeTypeConstructiveSolidGeometryID . There are five CSG object IDs:



 
kQ3SolidGeometryObjA

kQ3SolidGeometryObjB

kQ3SolidGeometryObjC

kQ3SolidGeometryObjD

kQ3SolidGeometryObjE

You specify the CSG operations to perform by passing a CSG equation to the Q3InteractiveRenderer_SetCSGEquation function. A CSG equation is a 32-bit value that encodes which CSG operations are to be performed on which CSG objects. QuickDraw 3D provides constants for some common CSG operations:



 
typedef enum TQ3CSGEquation {

    kQ3CSGEquationAandB                             = (int) 0x88888888,

    kQ3CSGEquationAandnotB                          = 0x22222222,

    kQ3CSGEquationAanBonCad                         = 0x2F222F22,

    kQ3CSGEquationnotAandB                          = 0x44444444,

    kQ3CSGEquationnAaBorCanD                        = 0x74747474

} TQ3CSGEquation;

For instance, the constant kQ3CSGEquationAandB indicates that the interactive renderer should render only the intersecting portion of the objects with CSG object IDs kQ3SolidGeometryObjA and kQ3SolidGeometryObjB . There are 2 32 CSG equations for the five possible CSG objects. You calculate a CSG equation for a particular configuration of objects A , B , C , D , and E by using Table 1 .

You calculate a CSG equation by determining which of the rows in the table satisfy the desired CSG construction. Then you set the indicated bit positions in a 32-bit value and clear the remaining bit positions. For instance, the value 1 appears in both of the columns for objects A and B for bit positions 3, 7, 11, 15, 19, 23, 27, and 31. The CSG equation, then, for the operation A B is 10001000100010001000100010001000, or 0x88888888 (kQ3CSGEquationAandB ). Similarly, the value 1 appears in the column for object A and the value 0 appears in the column for object B for bit positions 1, 5, 9, 13, 17, 21, 25, and 29. The CSG equation, then, for the operation A ¬ B is 00100010001000100010001000100010, or 0x22222222 (kQ3CSGEquationAandnotB ). Finally, the CSG equation used to construct the composite object shown in Figure 3 , drawn using the operation ( A B ) ¬ C , is 00110010001100100011001000110010, or 0x32323232.

Table 1 Calculating CSG equations
E 4	D 3	C 2	B 1	A 0	Object Bit position
0	0	0	0	0	0 LSB
0	0	0	0	1	1
0	0	0	1	0	2
0	0	0	1	1	3
0	0	1	0	0	4
0	0	1	0	1	5
0	0	1	1	0	6
0	0	1	1	1	7
0	1	0	0	0	8
0	1	0	0	1	9
0	1	0	1	0	10
0	1	0	1	1	11
0	1	1	0	0	12
0	1	1	0	1	13
0	1	1	1	0	14
0	1	1	1	1	15
1	0	0	0	0	16
1	0	0	0	1	17
1	0	0	1	0	18
1	0	0	1	1	19
1	0	1	0	0	20
1	0	1	0	1	21
1	0	1	1	0	22
1	0	1	1	1	23
1	1	0	0	0	24
1	1	0	0	1	25
1	1	0	1	0	26
1	1	0	1	1	27
1	1	1	0	0	28
1	1	1	0	1	29
1	1	1	1	0	30
1	1	1	1	1	31 MSB

Previous | QD3D Book | Overview | Chapter Contents | Next